AREA OF SQUARE USING DIAGONAL- MINDSPARK

Area of Square using Diagonal

A square is a quadrilateral with equal sides. A quadrilateral means a figure having four sides. A square has 4 sides where all the sides and angles are equal( 90°). The area of a square means the measure of the surface covered by the square, which is equal to the product of its two sides.

Area of Square =s \times s=s^{2}, where s is the side of the square.

Now, to find the area of a square using the diagonal we join two opposite vertices of the square as shown in the figure below where s is the length of the side of the square and d is the length of the diagonal.

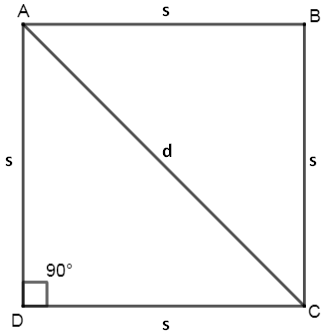
After joining A and C, two right-angled triangles are formed as we know the angles of a square are 90°.

In ΔADC, angle D =  90°, 

In a right-angled triangle, we can use Pythagoras Theorem which states that 

Here 

Base = s

Perpendicular = s and  Hypotenuse = d 

Therefore using Pythagoras we get 

s^{2}+s^{2}=d^{2}

\Rightarrow 2 s^{2}=d^{2}

\Rightarrow s^{2}=\left(d^{2}\right) / 2-(1)

Now we have the value of s in terms of d,

We know that Area of Square =s \times s=s^{2} \quad-(2)

Now putting the value of \mathrm{s}^{2} from (1) in (2)

We get 

Area of Square =s^{2}=\left(d^{2}\right) / 2

Therefore the area of a square using diagonal =\left(d^{2}\right) / 2

Examples

1. In a square, the length of the diagonal is 20 cm. Find the area of the square.

Area of the square using diagonal =d^{2} / 2

It is given that the length of the diagonal = 20 cm 

Therefore area of the square =20^{2} / 2=400 / 2=200 \mathrm{~cm}^{2}

2. The area of a square is50 \mathrm{~cm}^{2}Find the length of its diagonal.

Area of the square using diagonal =\mathrm{d}^{2} / 2

  It is given that area of the square 50 \mathrm{~cm}^{2}

50=d^{2} / 2

\Rightarrow d^{2}=50 \times 2

\Rightarrow d^{2}=100

\Rightarrow d=10 cm

  Therefore the length of the diagonal is 10 cm.