Area of a Cube with Example and FAQs

Area of a Cube 

A three-dimensional solid figure in which all its faces are of equal dimension and the length of its edges are all equal, i.e., all its faces are squares is called a cube. The area of a cube is the area that is enclosed by all the faces of the cube and it is calculated using the formula:

 Area of Cube = 6 \times a^{2} , where a is the length of the side of the cube.

The Surface Area of  Cube

The surface area of a cube can be of two types that are:

1. Total Surface Area
2. Lateral Surface Area

Total Surface Area

The total surface of a cube is the area enclosed by all the six faces in the cube.

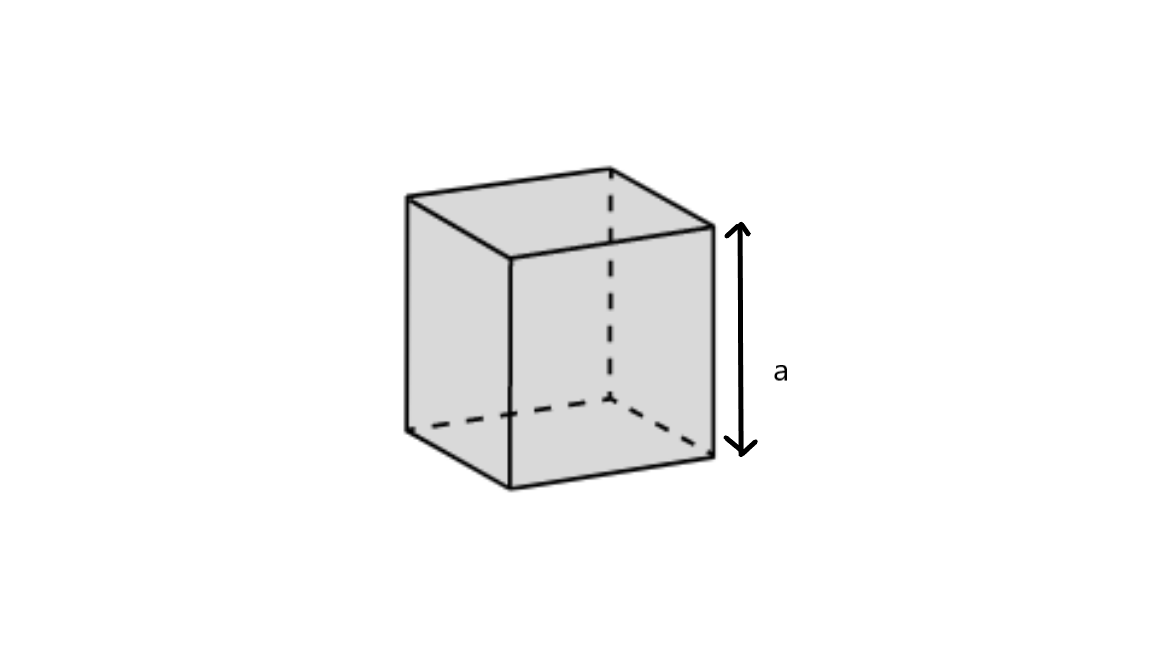
A Cube

For a cube with length ‘a’ the total surface area is actually the total area enclosed by the figure below:

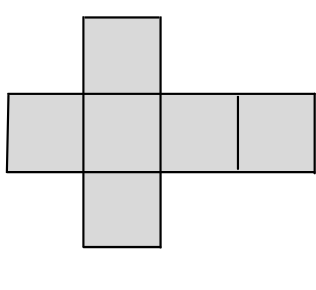
Total Surface Area of a Cube

Here the length of the side of each square is ‘a’ and there are 6 such squares. 

We know that area of a square = (length of side)^{2},

Hence the formula for the Total Surface Area is:

Total Surface area of cube =6 \times a^{2}=6 a^{2}

The unit of measurement of the area is ‘square units’. For example \mathrm{cm}^{2}, \mathrm{~m}^{2}, \text { etc. }

  
Lateral Surface Area

The lateral surface includes only the sides of the cube, i.e., it excludes the top and bottom of the cube. Hence, while calculating the lateral surface area, areas of the top and bottom faces are excluded.

For a cube with length ‘a’ the lateral surface area of the cube is the total area enclosed by the figure below:

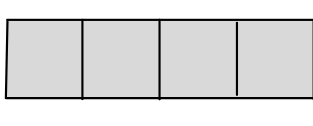
Lateral Surface Area of a Cube

Here the length of the side of each square is ‘a’ and there are 4 such squares. 

Hence the formula which gives the Lateral Surface Area of a cube is:

Lateral Surface Area =4 \times a^{2}=4 a^{2}

Examples

Example 1: The length of the side of the cube is 20 cm. Find the total and lateral surface areas of the cube.

Solution:

Given, length of the side of the cube, l = 20 cm

∴ The Total Surface area

=6 l^{2}

=\left(6 \times 20^{2}\right) \mathrm{cm}^{2}=2400 \mathrm{~cm}^{2}

And lateral surface area

=4 l^{2}

=\left(4 \times 20^{2}\right) \mathrm{cm}^{2}=1600 \mathrm{~cm}^{2}

Hence, the Total Surface Area is 2400 {cm}^{2} and Lateral Surface Area is 1600 {cm}^{2} .

Example 2: The total surface area of a cube is 60m^{2}. What is the length of each edge of such a cube?

Solution:

Let the length of the cube be x m

We know the Total Surface area =6 x^{2}=60 \mathrm{~m}^{2}

\therefore x^{2}=\frac{60}{6} m^{2}=10 m^{2}

\Rightarrow x=\sqrt{10} \mathrm{~m}

Therefore, the length of each side of the cube is \sqrt{10} \mathrm{~m}.